Overview

Statistical significance measures how unusual your experiment results would be if there were no difference in performance between your variation and baseline and the discrepancy in lift was due to random chance alone.

Hypothesis testing

Statistical significance is most practically used in hypothesis testing. For example, you want to know whether changing the color of a button on your website from red to green will result in more people clicking on it. If your button is currently red, that’s called your “null hypothesis,” which is your experiment baseline. Turning your button green is known as your “alternative hypothesis.”

To determine the observed difference in a statistical significance test, you will want to pay attention to two outputs: the p-value and the confidence interval.

• Confidence level (or P-value) can be defined as the likelihood of seeing evidence as strong or stronger in favor of a difference in performance between your variation and baseline, calculated assuming there is no difference between them and any lift observed is entirely owed to random fluke. P-values do not communicate how large or small your effect size is or how important the result might be.

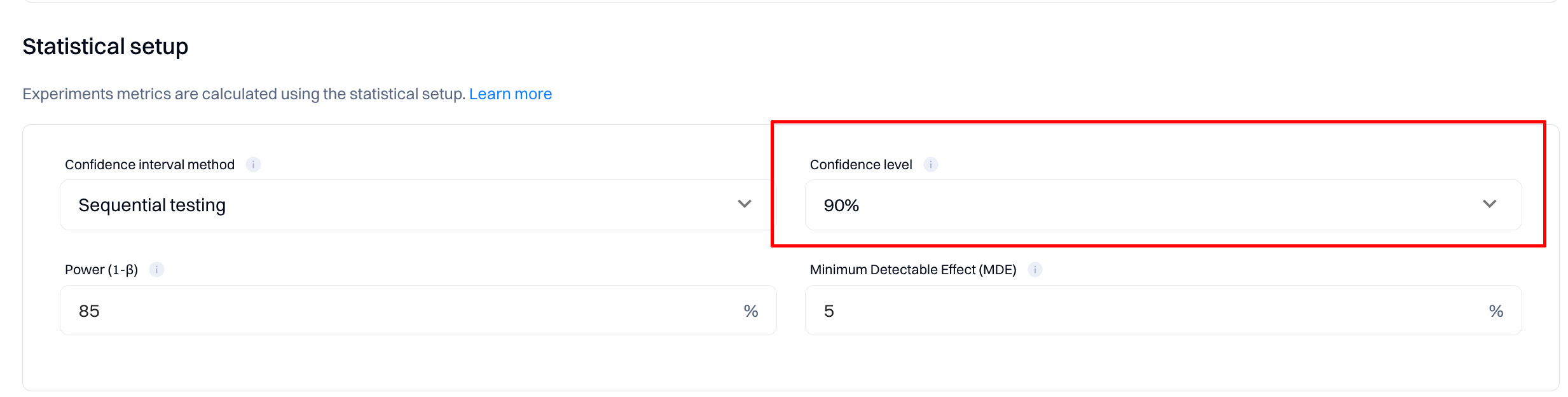
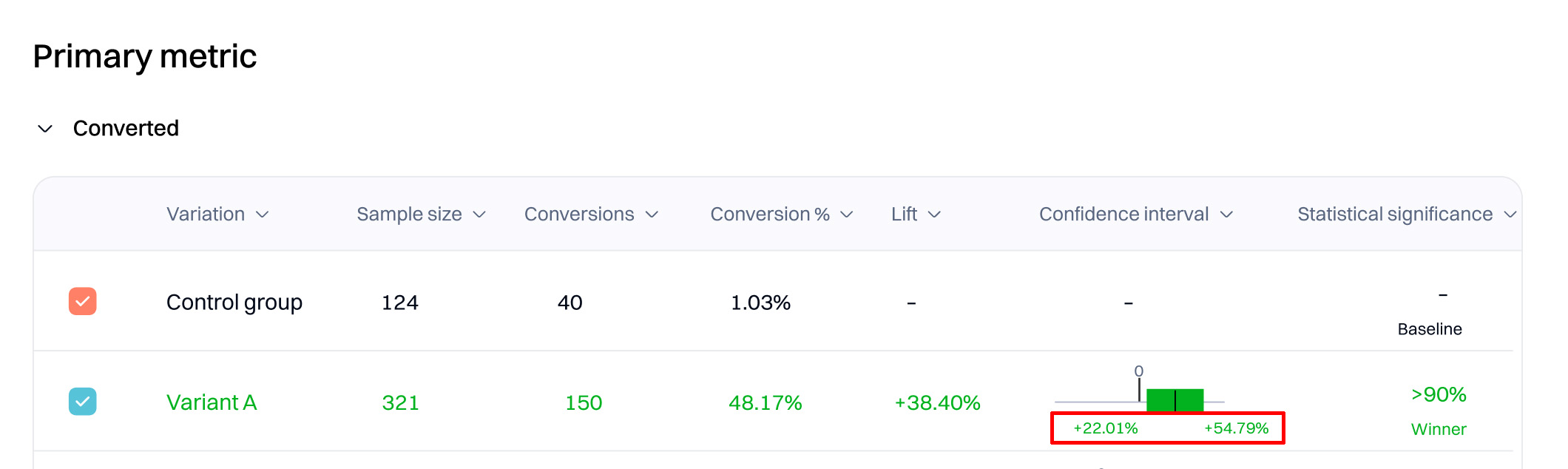
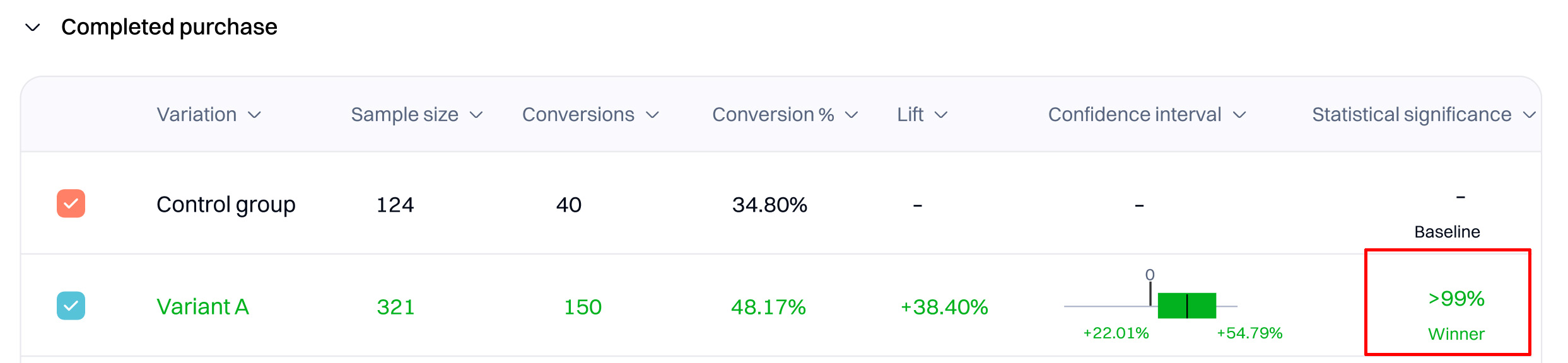
• Confidence interval refers to an estimated range of values that are likely, but not guaranteed, to include the unknown but exact value summarizing your target population if an experiment was replicated numerous times. An interval comprises a point estimate (a single value derived from your statistical model of choice) and a margin of error around that point estimate. Best practices are to report confidence intervals to supplement your statistical significance results, as they can offer information about the observed effect size of your experiment.

Why is statistical significance important?

Your metrics and numbers can fluctuate wildly from day to day. Statistical analysis provides a sound mathematical foundation for making business decisions and eliminating false positives. A statistically significant result depends on two key variables: sample size and effect size.

• Sample size refers to how large the sample for your experiment is. The larger your sample size, the more confident you can be in the result of the experiment (assuming that it is a randomized sample). If you are running tests on a website, the more traffic your site receives, the sooner you will have a large enough data set to determine if there are statistically significant results. You will run into sampling errors if your sample size is too low.
• Effect size refers to the magnitude of the difference in outcomes between the two sample sets and communicates the practical significance of your results.

Beyond these two factors, a key thing to remember is the importance of randomized sampling. If traffic to a website is split evenly between two pages, but the sampling isn’t random, it can introduce errors due to differences in the behavior of the sampled population.

For example, if 100 people visit a website and all the men are shown one version of a page and all the women are shown a different version, then a comparison between the two is not possible, even if the traffic is split 50-50, because the difference in demographics could introduce variations in the data. A truly random sample is needed to determine that the experiment's result is statistically significant.

Statistical significance in Intempt

When you observe a lift with 90% or higher statistical significance, the observed results are more unusual than expected in 90% of the cases if there is no lift. Assuming there was no difference in performance between the variation and the baseline, the higher your statistical significance, the more unusual your results would seem.

In statistics, you observe and use a population sample to infer the total population. Intempt experiments uses statistical significance to infer whether your variation caused movement in the metric.

Statistical significance helps control the rate of errors in experiments. In any controlled experiment, there are three possible outcomes:

Accurate results – When there is an underlying positive or negative difference between your original and your variation, the data shows a winner or loser. When there is not a difference, the data shows an inconclusive result.

False-positive (Type I Error) – Your test data shows a significant difference between your original and your variation, but there is random noise in the data—there is no underlying difference between your original and your variation.

False-negative (Type II Error) – Your test is inconclusive, but your variation differs from your baseline.

Statistical significance measures how likely your improvement is to be due to an actual change in underlying behavior instead of a false positive.

Lower significance levels may increase the likelihood of error but can also help you test more hypotheses and iterate faster. Higher significance levels decrease the error probability but require a larger sample.

Choosing the right significance level should balance the types of tests you are running, the confidence you want to have in the tests, and the amount of traffic you receive.

One-tailed and two-tailed tests

When you run a test, you can run a one-tailed or two-tailed test.

• Two-tailed tests – Detects the differences between the original and the variation in both directions. Two-tailed tests tell you if your variation is a winner and if your variation is a loser.
• One-tailed test – Tells you whether the variation is a winner or a loser, but not both. One-tailed tests detect differences between the original and the variation in only one direction.

Intempt experiments uses two-tailed tests because they are required for the false discovery rate control that Intempt has implemented in Statistics Engine. False discovery rate control is more important when making business decisions than using a one-tailed or two-tailed test because you want to avoid implementing a false positive or negative.

Changing statistical significance setting

You should know certain trade-offs associated with changing the statistical significance setting. In general:

• A higher significance setting is more accurate but requires a larger sample size, which increases the time required for Intempt experiments to declare significant results.
• A lower statistical significance level decreases the amount of time needed to declare significant results, but lowering the statistical significance setting also increases the chance that some results are false positives.

📘

Good to know

Changing your statistical significance setting instantly affects all currently running experiments. If your experiment has a goal with an 85% statistically significant winner, and you change your statistical significance setting from 90% to 80%, the next time you load your Experiment results page, you see a winner (85% > 80%). Your difference intervals also shrink to reflect the reduced need for confidence.